We all know this sequence of sounds:
It's called a scale and we take it for granted. But where did it come from? It didn't just fall out the sky, did it...?
To tell this story, we must enter the fascinating world of acoustics, the science of sound. Sound is generated by a vibration of the air (the presence of a mammalian ear being irrelevant, the old joke about a tree falling in a forest notwithstanding).
Get hold of a guitar or violin then pluck a string and watch closely. You can see the string thrumming the air. We call the number of times the string swings from all the way to one side to all the way to the other and back again to the starting point its frequency, measured in cycles per second. We also call this unit a hertz (Hz) after Heinrich Hertz, a smart German who proved beyond doubt that light and heat were electromagnetic wave phenomena (he is also the reason why radio waves are measured in hertz, i.e., the megahertz of the FM band and, for those of a certain age, the kilohertz of the AM band; not a bad achievement). Thus, a string that vibrates through its whole cycle 110 times every second produces a tone that is said to have a frequency of 110 Hz.
In our modern system, the tone generated at 110 Hz is among the many notes designated A, technically A2. I am using this particular note as our starting point because it will be most convenient arithmetically as we go along.
Before proceeding, we need take a moment to remember that the above discussion explicates a law of physics; obviously, the note name (A or B-flat or C-sharp or E, etc.) is a bit of cultural artifice, but the frequencies and resulting tones are decreed by Mother Nature in all her symmetrical beauty.
Now let’s travel back to ancient Greece, to the redoubtable Pythagoras (ca. 570 BC – ca. 495 BC), whose famous theorem we all had drilled into us in school. Pythagoras was the first great teacher we know of who obsessed over numbers: to him, the entire universe could be described using numbers. This obsession went so far that he founded a semi-religious cult in southern Italy[a] where the curriculum was based on this all-inclusive devotion to numbers. And, oh yes, that obsession extended to music.
Pythagoras may not have had a modern guitar or violin, but he did have a “monochord”, which is simplicity itself: it consists of a string tautened between two endpoints over a box that can give the vibrations some resonance. A search of the internet will produce any number of images of the monochord, both historic and modern reconstructions. Here’s one courtesy of Pinterest:
For a man capable of formulating the length of the hypotenuse, a question that would quite naturally occur to Pythagoras would be: what if I press the string onto the little wedge in the middle of the rail (the “bridge”), listen to the tones produced by the vibrations on each side, and determine how the tones relate based on how long the two string segments are?
Let's replicate Pythagoras’ method. If you pluck the second string from the top on a right-handed guitar (i.e., the second thickest one), you will produce the A2 I mentioned above, vibrating at 110 Hz (assuming the guitar has been tuned recently…). The ratio of the length of the whole string to itself is obviously one-to-one.
| Pythagoras' Ratios | |||||
| Ratio | Proportions | Frequencies | Notes | Modern interval name |
Greek interval name |
| 1 : 1 |  |
110 Hz : 110 Hz | A2 : A2 | unison | unison |
Now things start to get interesting. Press the string exactly in the middle and pluck the two halves. They are vibrating at exactly twice the rate as the whole string. Today we say the resulting note is an octave higher than the original; the Greeks called this interval a diapason.
| Pythagoras' Ratios | |||||
| Ratio | Proportions | Frequencies | Notes | Modern interval name |
Greek interval name |
| 1 : 1 | |
110 Hz : 110 Hz | A2 : A2 | unison | unison |
| 2 : 1 |  |
220 Hz : 110 Hz | A3 : A2 | octave | diapason |
[I dislike having to introduce the label “octave” at this point because it’s like giving away the punchline to a joke at the beginning; it implies an eight-way division, and we don’t get that until our story is well along.] This relationship can’t be emphasized enough: the two halves vibrate at exactly double the rate of the whole. This would be true no matter what string is plucked or how tight or loose it is.
At this point, we will stop concerning ourselves with the whole string, with the 110 Hz A2, because we want to examine the plucked subportions. The relationships of the smaller portions to the whole, called overtones, is the subject of a related but separate discussion.
Two halves vibrating at exactly twice the speed of the whole is fairly easy to understand. But Pythagoras made some very interesting discoveries as he continued to experiment. When he pressed the string where the lengths of the two portions were in a 3-to-2 ratio, he produced the most pleasing ("consonant") interval of all. The Greeks called it a diapente and we call it the perfect fifth. Rest assured that modern scientific instruments confirm that the speed of vibration of the two portions is also in a 3-to-2 ratio.
| Pythagoras' Ratios | |||||
| Ratio | Proportions | Frequencies | Notes | Modern interval name |
Greek interval name |
| 1 : 1 | |
110 Hz : 110 Hz | A2 : A2 | unison | unison |
| 2 : 1 | |
220 Hz : 110 Hz | A3 : A2 | octave | diapason |
| 3 : 2 |  |
330 Hz : 220 Hz | E3 : A3 | fifth | diapente |
To see why it’s called a fifth rather than a two-thirds or a three-halves, visualize a modern keyboard:
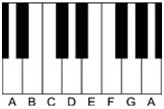
Musicians measure “intervals” (the distance between two tones) using inclusive counting, which is the practice of calculating the distance between two quantities as including the starting point, something we just don’t do in everyday life. Moving from A up to E you count off four keys, but if you include the starting note it’s five, and musicians call the resulting interval a fifth.
Inevitably, Pythagoras went on to test a 4-to-3 ratio of segment lengths and produced today's perfect fourth, another interval very pleasing to the ear, which he would have known as a diatessaron.
Look at the four ratios we’ve examined so far and bask in the simple mathematical beauty of it:
| Pythagoras' Ratios | |||||
| Ratio | Proportions | Frequencies | Notes | Modern interval name |
Greek interval name |
| 1 : 1 | |
110 Hz : 110 Hz | A2 : A2 | unison | unison |
| 2 : 1 | |
220 Hz : 110 Hz | A3 : A2 | octave | diapason |
| 3 : 2 | |
330 Hz : 220 Hz | E3 : A3 | fifth | diapente |
| 4 : 3 |  |
440 Hz : 330 Hz | A4 : E3 | fourth | diatessaron |
These, then, are the foundation stones of what’s termed functional harmony, which is what we call the system of chord progressions we take for granted today. To demonstrate: here is the scale most relevant to the intervals in the above chart (the pound sign, or for you younger folks the hashtag, means sharp):
The starting note is called the fundamental. The diatessaron above the fundamental is D and the diapente is E. Musicians refer to the notes of a scale with Roman numerals, so with this scale A, D and E are I, IV and V respectively. Any guitar or piano player who wants to harmonize a song written using this scale can use the three-note combinations (chords) built on those tones, viz.:
| Root of chord |
Component notes |
| I | A C# E |
| IV | D F# A |
| V | E G# B |
Well, would you look at that; every note in the scale appears in at least one of those chords. To repeat, those three chords are all you need to harmonize a song (and never lose sight of the fact that Nature herself has given us those chords). Plenty of amateur guitar players may not know any chords other than I, IV and V, but those are enough to harmonize any song. And ever since Pythagoras, those intervals have remained the most important in Western music. The octave, the fourth and the fifth reign.
This is the important thing to reaffirm at this point in the discussion: the music we hear today uses a harmonic system that is fundamentally grounded in a law of physics. Rather than take my word for it, ponder this bold statement:
“Pythagoras' study of the moving string and his discovery of the harmonic progression of simple whole numbers was the first real scientific work and creation of modern science.”[b]
How do we get from Pythagoras, who died 2,500 years ago, to the familiar pattern of white and black keys on a Steinway grand, a Fender Rhodes, a Hammond B3 or an imitation-Baroque Beckerath? Before Pythagoras had discovered any of the mathematical symmetries we’ve looked at already, his fellow Greeks had organized the tones into tetrachords (which sounds a lot like carbon tetrachloride, I know). A tetrachord wasn’t a group of four strings, it was a series of four notes that in Greek music always spanned the interval of the diatessaron (the 4:3 relationship). What about melodies that spanned a range greater than just a fourth? Two tetrachords could be joined, making an eight-note sequence (which finally brings us around to the OCTave). The resulting eight-note series was called a mode.[c] The Greeks gave each of their modes a name based on three regional/ethnic designations, namely, Dorian, Lydian and Phrygian; some required a prefix such as hypo or mixo. How can we (roughly) reproduce on a modern piano those long-ago modes? To answer that, we leave ancient Greece behind and plunge into the European Middle Ages.
Some of us will remember the brief flurry of enthusiasm in the early 1990s for Gregorian chant (referred to formally as plainchant[d]). Those chants (sung to this day in some Roman Catholic institutions) use the same patterns of intervals as the Greek modes. We can make the transition from Greece to the medieval monastery by refreshing our memories with the familiar keyboard:
Every passage between a black and a white key is termed a “half step”, while the interval between those white keys that have an intervening black key constitute a “whole step”. The difference is easily distinguishable, even by the untrained ear.
As we can see from our keyboard diagram, there are two cases in which the transition between white keys is only a half step, between E and F and between B and C. So in any sequence of eight continuous white keys, there will be, willy-nilly, five whole steps and two half steps. If we lay out every possible white-key-only sequence beginning on each of the seven white keys, we get the following combinations, roughly duplicating the ancient Greek modes (whole steps are represented by long dashes, half steps by hyphens):
That’s it. Those are the seven possible combinations.
The plainchant sung by Catholic monks could hardly help but be influenced by their inheritance of the Greek modes and the theoretical framework underlying them. Sometime during the Middle Ages, each of the Church modes got assigned one of the old Greek names (hypophrygian, mixolydian, etc.) but the process was completely arbitrary—unfortunately, today’s music historians have no way of knowing whether the Church got the name assignments right. For this reason, I will abjure the probably spurious Greek mode names[e] and stick with the official Catholic numbering system.
Let’s look again at the modes we laid out above alongside their official Church nomenclature:
There you have them, the seven (technically eight)[f] medieval Church Modes.
Picture the scene: a monastery in Europe in a scenic pasture bordered by woodlands sometime in the 11th century AD; take a moment to ponder the pure strangeness of it—a society so utterly different from ours. Eight times a day (each of these sessions was called an office), a bunch of monks stopped what they were doing and gathered in the chapel to sing plainchant (the offices known as vigil and matins required waking up the middle of the night). To paraphrase the legendary music historian Donald Jay Grout, throughout the Middle Ages the most educated men in Europe spent a significant part of their adult lives singing plainchant.
So, the years ticked along, with the Christendom dreamed of by Augustine of Hippo passing the identical centuries, one after another, the people endlessly praising God and hoping for Heaven and the monks singing their modes.
“Musicians in the early seventeenth century still thought of themselves as working within the eight church modes…”[g]
But not all the modes could survive: a great transition was underway. By the time of Johann Sebastian Bach (1685–1750), the first great composer most of the classically educated public is familiar with, five of the modes had fallen by the wayside (outside of the Church, anyway). After a millennium and a half of experience, only Mode VI and a modified version of either Mode I or II survived, standing triumphant at the dawn of the Modern Era, considered by composers perfectly adequate to fulfill their aesthetic goals. It’s just that, by Bach’s day, they were no longer called Mode VI and Mode I/II: they were called, respectively … the major and minor scales.
“By the last third of the [seventeenth] century, [Arcangelo] Corelli, [Jean-Baptiste] Lully and other composers were writing music we would unhesitatingly call tonal, operating within the system of major and minor keys…”[g]
The burning question, of course, is, Why these two? A clue can be found in Mode VI, which has come down to us interval-for-interval as the major scale. Notice that the final step is half one. The allure of the final transition being a half step proved to be irresistible. The provenance of the minor scale demonstrates this phenomenon. Unfortunately, the scale we call minor cannot be reproduced on the modern keyboard using only while keys. This is because the best you can do with white keys is what musicians call the natural minor (Mode II):
A — B - C — D — E - F — G — A
Change the final step to a half one and you get this hybrid, called by musicians the harmonic minor:
A — B - C — D — E - F — - G# - A
This was not going to work in practice because the giant step-and-a-half between F and G sharp was simply not acceptable to anybody. To solve this, the sixth note of the scale was bumped up by a half step, resulting in today’s melodic minor, which we accept as THE minor scale:
A — B - C — D — E — F# — G# - A
Each note is called a degree of the scale and theoreticians have, as is their wont, assigned names to these degrees:
It is perhaps significant that the only note without a Latinoid name is that last one: its function is merely to “lead” to the triumphant return of the tonic an octave above the original.
As the succeeding centuries have amply demonstrated, there is something irresistible about that half-step slide up to the higher tonic. Its employment was endorsed by a theoretician with the improbable name of Prosdocimo de’ Beldomandi (died 1428): if a half step is more pleasing to the ear than what’s written, go ahead and sing it. This practice was one of several referred to by the umbrella term musica ficta, literally fictitious music, i.e., singing some note other than the one provided by the composer. Prosdocimo was codifying the relentless trend toward making the final interval of any mode a half step that had long exerted its grip on monastic singers.
So, there we are. Even though seven sequences are available, today we only use two of them, because the modes that European composers did not find appealing just didn’t make the cut. Let’s dream a what-if: how different would Western Music, hell, World Music, be today if, say, Modes III or IV had survived, the ones that begin with a half step (these are the ones the Greeks were afraid might cause insanity)? What strange sound worlds have we missed out on by jettisoning those five modes? Well, it’s too late now: the topic was settled once and for all around the time that the Glorious Revolution brought William and Mary to the throne of the United Kingdom.
“[Jean-Philippe] Rameau’s Treatise on Harmony in 1722 offered the first complete theoretical formulation of the new system, which by then had existed in practice for over half a century.”[g]
To summarize, our two modern scales go like this:
The modern world has voted with its ears: the Western two-mode system of music is everywhere. The major and minor scales, those scales we are so accustomed to that we don’t notice them any more than fish notice water, are the direct descendants of the sixth and (first or) second medieval Church Modes sung by countless monks over hundreds and hundreds of years.
On behalf of all those monks I'd just like to say, You’re welcome.
[a] At the time, southern Italy was called Magna Graecia (“Great Greece”), so even though it’s Italy geographically, culturally we can still say we’re in ancient Greece.
[b] Thomas Váczy Hightower, “The Creation of Musical Scales from a mathematic and acoustic point of view, Part II”, 2009
[c] As I alluded to earlier, the Greeks deeply respected the power of music; they actually believed it was capable of influencing human character. Plato worried that listening to too much of it in certain modes could cause moral degeneracy.
[d] The term "Gregorian chant" is not really appropriate. Pope Gregory the First did not write any chant himself, but the Church has historically attributed the process of organizing and codifying the chant corpus to him. The name sticks.
[e] European composers continued to use the Greek names into the Renaissance.
[f] In fact, the medieval Church recognized a total of eight modes, but the distinguishing feature of Mode VIII is beyond the scope of today’s lecture.
[g] Burkholder, Grout and Palisca, A History of Western Music, W.W. Norton, 17th ed., p. 306